A Red-Black Tree Implementation with Provable Properties

We algorithms people usually go trough great lengths to prove properties of our algorithms, for example, that they are correct, and that they run in \(O(...)\) time, etc. Unfortunately, we hardly ever implement our algorithms, and even if we implement them, we mostly forget about our proofs. So who is to say that our implementation actually has all these nice properties? Wouldn’t it be nice if our implementation came with its own proofs, showing that it is correct? This page shows how we can use the type system of our programming language to provide proofs of properties of our algorithm. In particular, we will show how we can use Haskell’s type system to enforce several properties of Red-Black trees.

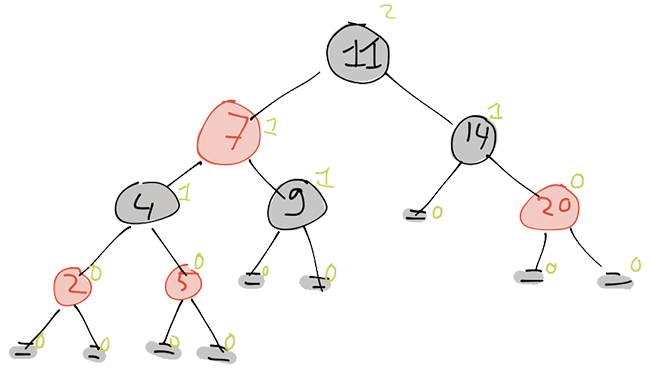
A Red-Black tree is a well known data structure to store an ordered sequence of values. It is a balanced binary search tree that stores values in its internal nodes. Each node has a color, either red or black, and there are some invariants that guarantee that a Red-Black tree is balanced. The five invariants are

1. every node is red or black,
2. the root is black,
3. every leaf is black,
4. if a node is red, then both its children are black, and
5. for each node, the black-height of the left child is the same as the black-height of the right child. The black height is the number of black nodes on a path from the node to a leaf.

We will use Haskell’s type system to enforce these invariants. Our implementation will use some of the, fairly new, features/extentions in GHC:

{-# LANGUAGE DataKinds #-}
{-# LANGUAGE KindSignatures #-}
{-# LANGUAGE GADTs #-}

This page is written as as literate haskell. The complete source code can be found here.

module RedBlackTree where

import Control.Applicative((<$>))

Defining Data Types

We start by defining a type representing the colors. We will not construct values of the type color at all, instead we will use Red and Black only as types, and Color only as a kind. Hence, we do not bother deriving instances for type classes such as Show and Eq.

data Color = Red | Black

The same for type level natural numbers. For now we will roll out our own Nat kind, which just models Peano numbers. GHC 7.8 has proper support for type level natural numbers, so then we can instead use 0, 1, 2, … as types. Until then, we will use this instead.

data Nat = Z | S Nat

Now onto the real stuff. A data type representing a node in our tree. Nodes are parameterized by three things: their color (of kind Color), their black height (of kind Nat), and the type of the values that are stored (of kind *). The color and the black-height are “Phantom types”. They don’t (directly) influence the data that is stored. Instead, they are only used to enforce our invariants: For example, the associated color phantom-type immediately enforces invariant 1): Each node has a color, and since its kind is Color, this is either Red or Black.

data Node (c :: Color) (h :: Nat) (a :: *) where
  Leaf  ::                                          Node Black Z     a
  -- 3) Every leaf is black (and has black height 0)
  BNode :: Node lc    h a -> a -> Node rc    h a -> Node Black (S h) a
  -- 5) The black height left and right is the same.
  --    Adding a black node increases the black height
  RNode :: Node Black h a -> a -> Node Black h a -> Node Red   h     a
  -- 4) If a node is red, its children must be black

As we can see, a Node is either a Leaf, a BNode, or a RNode. Leaves are black (invariant 3), and have black-height zero. A BNode (black node) can be constructed from a left child, a value, and a right child. There are no restrictions on the colors of the left and right child, and they may even differ. However, we do enforce that the black height of both children is the same: namely h (invariant 5). Since this node itself is black as well, we produce a ndoe of black-height h + 1. The Red RNodes have the same structure as the BNodes, however, we not only enforce that the children have the same black-height, but also that they are both black!

The invariant we have not enforced yet is invariant 2: the root of a red black tree must be black. So, we introduce a type RedBlackTree that models a proper Red-Black tree, whose root is black, and hides the black-height phantom type from the user:

data RedBlackTree (a :: *) where
  Tree :: Node Black h a -> RedBlackTree a

The RedBlackTree type enforces all our invariants. Hence, if an operation returns something of type RedBlackTree: it is guaranteed that all invariants hold. Hence, the result is a proper Red-Black tree.

Inserting Into Red-Black Trees

Construction an empty red black tree is trivial.

empty :: RedBlackTree a
empty = Tree Leaf

Let’s see if we can also insert elements, so we can construct more interesting trees. To do so, we introduce some more types :D

When we insert something into a subtree rooted at a black node, the color of the root may change to red, thus potentially invalidating an invariant. To distinguish between the two cases (whether or not the root of the (sub)tree is indeed black) we have two cases. BDone, that tells us that the root is still black (and that all other invariants hold as well), or NewRed, which tells us that the insert required us to color this node red (but it is a proper red-node: so all our invariants (except invariant 2) hold for this subtree).

data BlackInsert (h :: Nat) (a :: *) where
  BDone  :: Node Black h a -> BlackInsert h a
  NewRed :: Node Red   h a -> BlackInsert h a

When we insert into a red node, we end up with a proper RedBlack tree with a red node as root (RDone), or a red node that has a red child:

data RedInsert (h :: Nat) (a :: *) where
  RDone    :: Node Red   h a -> RedInsert h a
  RedRed   :: RedRed     h a -> RedInsert h a

Since we cannot construct a red Node with a Red child. We introduce the RedRed data type, which models a red node in which one of its children is also red. Note that the type enforces that only one of the children violates invariant 4, not both, and that all other invariants still hold (i.e. that the black-height of both subtrees is the same).

data RedRed (h :: Nat) (a :: *) where
  LeftR  :: Node Red   h a -> a -> Node Black h a -> RedRed h a
  RightR :: Node Black h a -> a -> Node Red   h a -> RedRed h a

Also note that the children of the red child do form a proper red-black tree, so the only violation is in the current node.

If we want to insert something into a node whose color we do not know (such as for the children of a Black node). We do not know if we get something of type BlackInsert, or of type RedInsert. Hence, we introduce a new type InsertN that captures this:

data InsertN (h :: Nat) (a :: *) where
  RIns  :: RedInsert   h a -> InsertN h a
  BIns  :: BlackInsert h a -> InsertN h a

Now that we have all these data types, we can actually implement inserting an element into a subtree. We start with the most general case, in which we do not know the color of the node. In this case, we determine what sort of node we have, and delegate the insert to an other function.

insertN                   :: Ord a => a -> Node c h a -> InsertN h a
insertN x n@Leaf          = BIns $ insertL x n
insertN x n@(BNode _ _ _) = BIns $ insertB x n
insertN x n@(RNode _ _ _) = RIns $ insertR x n

Inserting something in a leaf creates a new red node. Furthermore, note that leaves specifically have black height zero.

insertL        :: a -> Node Black Z a -> BlackInsert Z a
insertL x Leaf = NewRed $ RNode Leaf x Leaf

Inserting into a red node is also easy: we know that our children are black, so we just use insertB on the proper child to do the actual inserting. If it turns out that the child is still black after inserting then we are happy because we are done. We simply tell our parent and that is it.

If turns out that the child has become red then we are being lazy: when we started the tree was a proper red-black tree which did not have any red nodes with red children. Hence, my parent must be black. So, we are just going to tell it that we are in trouble and we let it figure out how to deal with the problem.

insertR                 :: Ord a => a -> Node Red h a -> RedInsert h a
insertR x (RNode l y r)
  | x <= y              = case insertB x l of
                            BDone  l' -> RDone  $ RNode l' y r
                            NewRed l' -> RedRed $ LeftR l' y r
  | otherwise           = case insertB x r of
                            BDone  r' -> RDone  $ RNode  l y r'
                            NewRed r' -> RedRed $ RightR l y r'

Inserting in a black node is the most complicated. For two reasons: 1) we don’t know what color our children are, and 2) if we happen to have red children, then they might force their problems onto us. So, we have a few cases that we have to handle. Let’s start with the easy ones.

The first and third cases in the case statement on insertN are easy: all the interesting stuff happened somewhere down the tree, and currently we are only walking back up the tree plugging in the updated child.

The second case is where the interestingness stops (or starts, depending on your viewpoint ;)): inserting the new value in the child caused it to be recolored. However, since its black-height is still the same, and since we are a black node ourselves, we can remain a black node. This also means that for everything further up the tree the colors will remain the same.

The (only) interesting case is the last one: after inserting the new value, we ended up with a RedRed violation in that child, so we have to do some work to restore the invariants. The balanceL and balanceR functions which we will see next take care of that work. However, in doing so they have to color the current node red. Hence, we “tell our parent” that we have become red.

insertB :: Ord a => a -> Node Black h a -> BlackInsert h a
insertB x n@Leaf        = insertL x n
insertB x (BNode l y r)
  | x <= y              = case insertN x l of
              BIns (BDone  l') -> BDone  $ BNode    l' y r
              BIns (NewRed l') -> BDone  $ BNode    l' y r
              RIns (RDone  l') -> BDone  $ BNode    l' y r
              RIns (RedRed l') -> NewRed $ balanceL l' y r
  | otherwise           = case insertN x r of
              BIns (BDone  r') -> BDone  $ BNode    l  y r'
              BIns (NewRed r') -> BDone  $ BNode    l  y r'
              RIns (RDone  r') -> BDone  $ BNode    l  y r'
              RIns (RedRed r') -> NewRed $ balanceR l  y r'

Note that insertB promisses that the black height remains the same. So in particular, we we recolor this node from black to red, then the black-height of both children must increase. Indeed, the balanceL and balanceR functions take a left and right child (one of which violates the Red-Red invariant) of height h'=h-1, and produces a red node whose height is h'+1=h.

balanceL takes a RedRed as the left child, a value, and a proper subtree (of which we don’t care what color its root has) and we construct a new Red node. This is essentially a left-rotate in which we color the new root red, and the two children black. See Figure 2 for an illustration.

balanceL :: RedRed h a -> a -> Node c h a -> Node Red (S h) a
balanceL (LeftR (RNode lll llx llr) lx lr)  x r = RNode l' lx r'
    where
      l' = BNode lll llx llr
      r' = BNode lr  x   r
balanceL (RightR ll lx (RNode lrl lrx lrr)) x r = RNode l' lrx r'
    where
      l' = BNode ll  lx   lrl
      r' = BNode lrr x    r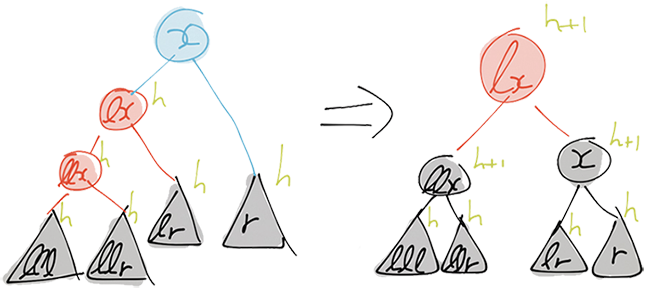

balanceR is it’s symmetric companion which does a right-rotate and a recoloring.

balanceR :: Node c h a -> a -> RedRed h a -> Node Red (S h) a
balanceR l x (LeftR (RNode rll rlx rlr) rx rr)  = RNode l' rlx r'
    where
      l' = BNode l   x   rll
      r' = BNode rlr rx  rr
balanceR l x (RightR rl rx (RNode rrl rrx rrr)) = RNode l' rx r'
    where
      l' = BNode l   x    rl
      r' = BNode rrl rrx  rrr

So now that we know how to insert something into a node. Inserting into a RedBlackTree is easy:

insert            :: Ord a => a -> RedBlackTree a -> RedBlackTree a
insert x (Tree n) = case insertB x n of
                      BDone  bn -> Tree bn
                      NewRed rn -> Tree $ turnBlack rn

turnBlack makes sure that the root is black: if the insert would have returned a subtree rooted at a red node, we recolor it.

turnBlack               :: Node Red h a -> Node Black (S h) a
turnBlack (RNode l x r) = BNode l x r

Now that we know how to insert one node, we can of course also insert many of them:

insertAll :: Ord a => [a] -> RedBlackTree a -> RedBlackTree a
insertAll = flip (foldr insert)

Deleting Elements

Everyone can do insertions into Red-Black trees. So let’s do deletions as well. We again start by defining data types. After inserting an element into the tree we observed that after inserting the element the black-height either stayed the same, or it increased by one. When we remove an element, we see the reverse: either the height stays the same, or it is decreased by one.

If we delete something from a subtree rooted at a red node, we can locally fix the problem, and increase the height to its original value, by coloring the root black. Hence, we represent the result of deleting something from a red-subtree by the following data type.

data RedDelete (h :: Nat) (a :: *) where
  RDeleted :: Node Red   h a -> RedDelete h a
  NewBlack :: Node Black h a -> RedDelete h a

If we remove something from a black subtree, we cannot use this trick of recoloring the root. So this is the place where we may end up with a subtree that is too shallow. We expres this in the BlackDelete data type.

data BlackDelete (h :: Nat) (a :: *) where
  BDeleted :: Node Black h a -> BlackDelete h a
  BShallow :: Node Black h a -> BlackDelete (S h) a

The type signature of the BShallow is best interpeted as: if you give me a black node of height h, I can pretend to be a BlackDelete of height h+1. We also add some shorthands to construct RedDelete and BlackDelete values:

rDeleted :: Node Black h a -> a -> Node Black h a -> RedDelete h a
rDeleted l x r = RDeleted $ RNode l x r

newBlack       :: Node lc h a -> a -> Node rc h a -> RedDelete (S h) a
newBlack l x r = NewBlack $ BNode l x r

bDeleted :: Node lc h a -> a -> Node rc h a -> BlackDelete (S h) a
bDeleted l x r = BDeleted $ BNode l x r

Now that we have the data types, let’s start with the easiest case. Deleting something from a red subtree. Once we have found the node containing the element that we want to delete, we distinguish two cases. If this subtree does not contain any other elements, i.e. if its left and right children are leaves. We can easily delete the element: we simply return a leaf, which has the same black-height as our original subtree, wrapped in a NewBlack constructor.

If however we want to delete an element in an internal node, we extract the smallest element m in the right subtree, and replace the value in the current node by m.

deleteR    :: Ord a => a -> Node Red h a -> RedDelete h a
deleteR x (RNode l y r)
  | x == y = case (l, r) of
               (Leaf, Leaf)        -> NewBlack Leaf
               (_,    BNode _ _ _) -> let (m,r') = extractMinB r in
                                      redDeleteRight l m r'
  | x <  y = redDeleteLeft  (deleteB x l) y r
  | x >  y = redDeleteRight l             y (deleteB x r)

We will cover extractMinB (and its counterpart extractMinR) later. The redDeleteRight and redDeleteLeft functions are convienience functions to construct new RedDelete values. redDeleteLeft takes a BlackDelete value representing left child after deleting an element, a value, and a right child, and constructs a new node wrapped in a RedDelete. The redDeleteRight function is symmetric.

redDeleteLeft              :: BlackDelete h a -> a -> Node Black h a
                           -> RedDelete h a
redDeleteLeft (BDeleted l) = rDeleted    l
redDeleteLeft (BShallow l) = redBalanceL l

redDeleteRight :: Node Black h a -> a -> BlackDelete h a
               -> RedDelete h a
redDeleteRight l x (BDeleted r) = rDeleted    l x r
redDeleteRight l x (BShallow r) = redBalanceR l x r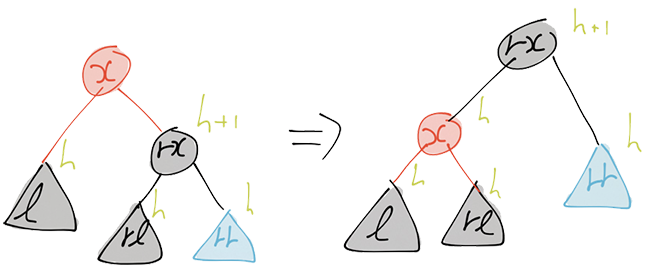

If the left subtree after deletion is of the form BDeleted _ we can directly reconstruct the current node. However, if the left subtree after deletion is too shallow, i.e. it only has black-height h-1, then we have to rebalance the tree in order to construct a proper subtree. The redBalanceL and redBalanceR functions take care of this.

redBalanceL                     :: Node Black h a -> a -> Node Black (S h) a
                                -> RedDelete (S h) a
redBalanceL l x (BNode rl rx rr) = case rl of
    Leaf        -> blackCase rl
    BNode _ _ _ -> blackCase rl
    RNode _ _ _ -> let l' = RightR   l x rl in
                   RDeleted $ balanceL l' rx rr
  where
    blackCase rl' = let l' = RNode l x rl' in
                    newBlack l' rx rr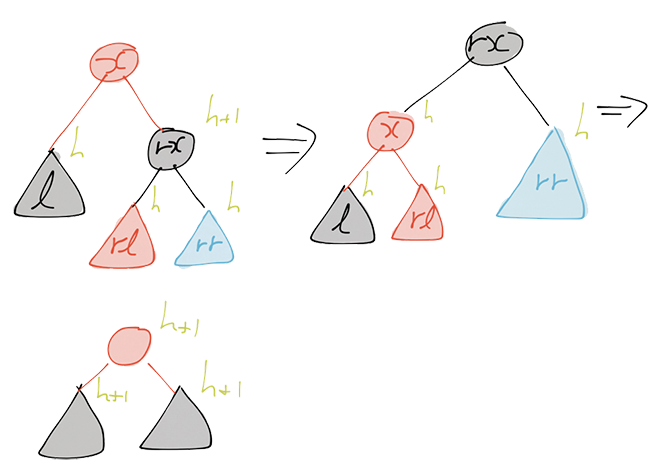

The operations of redBalanceL are depicted in Figures 3 and 4. In case rl is black, a simple left-rotate suffices. In case rl is red we also do a left-rotate. This leads to a red-red subtree, which we fix using the balanceL function. The function redBalanceR is symmetric:

redBalanceR :: Node Black (S h) a -> a -> Node Black h a
            -> RedDelete (S h) a
redBalanceR (BNode ll lx lr) x r = case lr of
    Leaf        -> blackCase lr
    BNode _ _ _ -> blackCase lr
    RNode _ _ _ -> let r' = LeftR lr x r in
                   RDeleted $ balanceR ll lx r'
  where
    blackCase lr' = let r' = RNode lr' x r in
                             newBlack ll lx r'

To delete an element in a black subtree we essentially use the same approach as before. However, since we do not know the color of the children, we have a few more cases to consider, which makes our code slightly more messy.

deleteB :: Ord a => a -> Node Black h a -> BlackDelete h a
deleteB _ Leaf          = BDeleted $ Leaf
deleteB x (BNode l y r)
  | x == y = case (l, r) of
        (Leaf,              Leaf             ) -> BShallow Leaf
        (Leaf,              RNode Leaf z Leaf) -> bDeleted Leaf z Leaf
        (RNode Leaf z Leaf, Leaf             ) -> bDeleted Leaf z Leaf
        (_,                 RNode _ _ _      ) ->
                                            let (m,r') = extractMinR r in
                                            blackDeleteRightR l m r'
        (_,                 BNode _ _ _      ) ->
                                            let (m,r') = extractMinB r in
                                            blackDeleteRightB l m r'
  | x <  y = case l of
        Leaf        -> blackDeleteLeftB  (deleteB x l) y r
        BNode _ _ _ -> blackDeleteLeftB  (deleteB x l) y r
        RNode _ _ _ -> blackDeleteLeftR  (deleteR x l) y r
  | x >  y = case r of
        Leaf        -> blackDeleteRightB l             y (deleteB x r)
        BNode _ _ _ -> blackDeleteRightB l             y (deleteB x r)
        RNode _ _ _ -> blackDeleteRightR l             y (deleteR x r)

In the case both l and r are leaves, the black-height of the tree after deletion –a single leaf– has black-height zero, whereas black-height one is required. Thus, we use our BShalow constructor. In the other two leaf cases there is still one remaining value in the subtree, one that is stored at a red node. We can “recolor” this node black to obtain something of black-height one. The final two cases for when x == y we again extract the minimum value m in the right subtree, and replace the value stored in this node by m.

In the cases that x < y or x > y, we delete the value in the appropriate subtree. We need the pattern matching on l and r to convince the compiler that these subtrees have the right color for us to use the blackDelete functions.

As with the deletes in Red subtrees, we have a few functions that describe how to construct a new BlackDelete value from a left-subtree in which an element is deleted, an element that we wish to store in the current node, and a regular right subtree. These functions are fairly straight forward: if one of the subtrees (after deletion) is a BShallow we rebalance, and otherwise we directly recmobine and construct a BlackDelete value using the BDeleted constructor.

blackDeleteLeftB              :: BlackDelete h a -> a -> Node rc h a
                              -> BlackDelete (S h) a
blackDeleteLeftB (BDeleted l) = bDeleted      l
blackDeleteLeftB (BShallow l) = blackBalanceL l

blackDeleteLeftR              :: RedDelete h a -> a -> Node rc h a
                              -> BlackDelete (S h) a
blackDeleteLeftR (RDeleted l) = bDeleted l
blackDeleteLeftR (NewBlack l) = bDeleted l

And of course we also have these functions in case we deleted something in the right subtree instead.

blackDeleteRightB :: Node rc h a -> a -> BlackDelete h a
                  -> BlackDelete (S h) a
blackDeleteRightB l x (BDeleted r) = bDeleted      l x r
blackDeleteRightB l x (BShallow r) = blackBalanceR l x r

blackDeleteRightR :: Node rc h a -> a -> RedDelete h a
                  -> BlackDelete (S h) a
blackDeleteRightR l x (RDeleted r) = bDeleted l x r
blackDeleteRightR l x (NewBlack r) = bDeleted l x r

The most difficult part is rebalancing in black nodes. We balance based on the color of the node.

blackBalanceR                 :: Node c (S h) a -> a -> Node Black h a
                              -> BlackDelete (S (S h)) a
blackBalanceR l@(BNode _ _ _) = blackBalanceRB l
blackBalanceR l@(RNode _ _ _) = blackBalanceRR l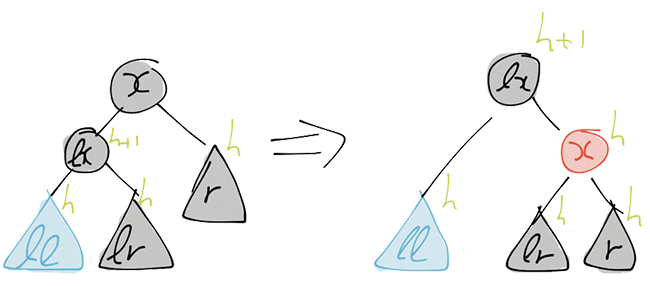

The actual balancing operations are best explained using figures. In both variants blackBalanceR, we do a right-rotate. Based on the color of a particular subtree this may introduce a RedRed subtree, which we fix using another rebalancing operation. See Figures 5 and 6 for the operation of blackBalanceRB.

blackBalanceRB :: Node Black (S h) a -> a -> Node Black h a
               -> BlackDelete (S (S h)) a
blackBalanceRB (BNode ll lx lr) x r = case lr of
    Leaf        -> blackCase lr
    BNode _ _ _ -> blackCase lr
    RNode _ _ _ -> let r' = LeftR lr x r
                       t  = balanceR ll lx r'
                   in BDeleted $ turnBlack t
  where
    blackCase lr' = let r' = RNode lr' x r
                    in BShallow $ BNode ll lx r'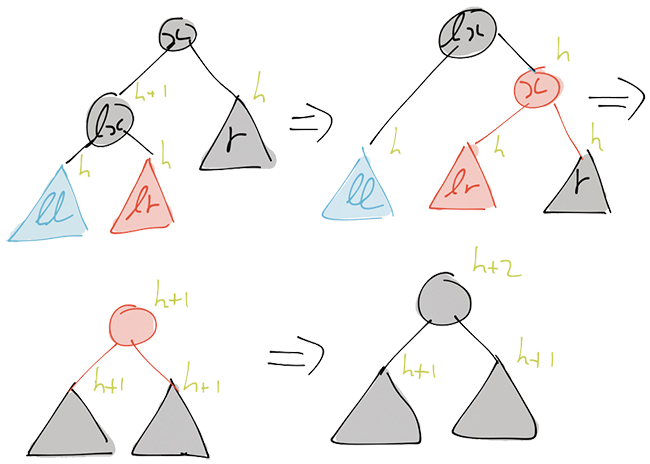

blackBalanceRR handles the case that we want to construct a black node of height h+2, but our right subchild is of height only h, and our left child is red. We again do a right-rotation and recoloring that is depicted in Figures 7 and 8.

blackBalanceRR :: Node Red (S h) a -> a -> Node Black h a
               -> BlackDelete (S (S h)) a
blackBalanceRR (RNode ll lx (BNode lrl lrx lrr)) x r = case lrr of
    Leaf        -> blackCase lrr
    BNode _ _ _ -> blackCase lrr
    RNode _ _ _ -> let rr' = LeftR lrr x r
                       r'  = balanceR lrl lrx rr'
                   in bDeleted ll lx r'
  where
    blackCase lrr' = let rr' = RNode lrr' x r
                         r'  = BNode lrl lrx rr'
                     in bDeleted ll lx r'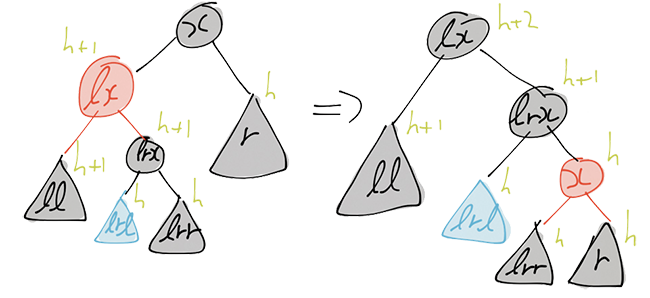

Again we have symmetric balancing functions for left-rotates that we use when we deleted stuff in the left subtree. > blackBalanceL :: Node Black h a -> a -> Node c (S h) a > -> BlackDelete (S (S h)) a > blackBalanceL l x r@(BNode _ _ ) = blackBalanceLB l x r > blackBalanceL l x r@(RNode _ _) = blackBalanceLR l x r

blackBalanceLB :: Node Black h a -> a -> Node Black (S h) a
               -> BlackDelete (S (S h)) a
blackBalanceLB l x (BNode rl rx rr) = case rl of
    Leaf        -> blackCase rl
    BNode _ _ _ -> blackCase rl
    RNode _ _ _ -> let l' = RightR l x rl
                       t  = balanceL l' rx rr
                       in BDeleted $ turnBlack t
  where
    blackCase rl' = let l' = RNode l x rl'
                    in BShallow $ BNode l' rx rr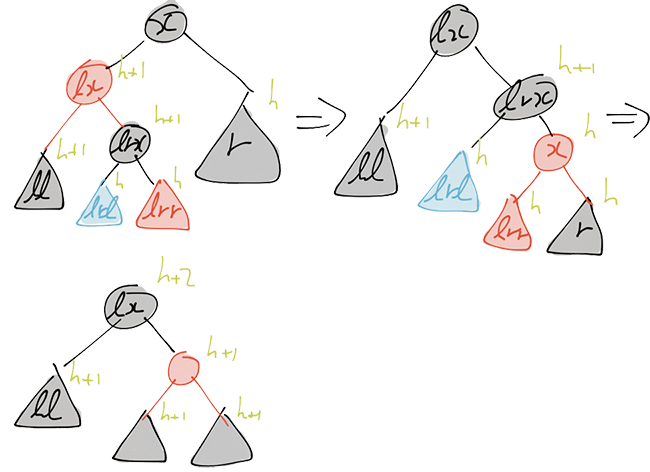

blackBalanceLR :: Node Black h a -> a -> Node Red (S h) a
               -> BlackDelete (S (S h)) a
blackBalanceLR l x (RNode (BNode rll rlx rlr) rx rr) = case rll of
    Leaf        -> blackCase rll
    BNode _ _ _ -> blackCase rll
    RNode _ _ _ -> let ll' = RightR l x rll
                       l'  = balanceL ll' rlx rlr
                   in bDeleted l' rx rr
  where
    blackCase rll' = let ll' = RNode l x rll'
                         l'  = BNode ll' rlx rlr
                     in bDeleted l' rx rr

Recall that to delete a (value in a) non-leaf node n, we actually extracted the smallest element m from the right subtree of n and replaced the value in n by m. We used the functions extractMinR and extractMinB to extract this minimum. So what remains is to actually implement these functions. Extracting an element is fairly similar to deleting one, so we can reuse a large part of the code we have already seen. Let’s start with extracting the minimum from a red node:

extractMinR                :: Node Red h a -> (a, RedDelete h a)
extractMinR (RNode Leaf            x r) = (x, NewBlack r)
extractMinR (RNode l@(BNode _ _ _) x r) =
  (\l' -> redDeleteLeft l' x r) <$> extractMinB l

In case the left child of the current (red) node is a leaf, this node contains the minimum. So we return it, and the remainder of this subtree, that is, the right child. Otherwise, the left subtree is a black, non-leaf, node so we can extract the minimum in that subtree using the function extractMinB. This produces a tuple (m,l') with the minimum m and the remainder of the left subtree l'. We use the <$> operator to apply the redDeleteLeft function on this second element of the tuple, the remainder l', and combine it with our right child to produce a subtree without element m. The `extractMinB’ function that extracts the minimum from a black subtree works analogously.

extractMinB :: Node Black (S h) a -> (a, BlackDelete (S h) a)
extractMinB (BNode Leaf x r)            = case r of
  Leaf        -> (x, BShallow r)
  RNode _ _ _ -> (x, BDeleted $ turnBlack r)
extractMinB (BNode l@(BNode _ _ _) x r) =
  (\l' -> blackDeleteLeftB l' x r) <$> extractMinB l
extractMinB (BNode l@(RNode _ _ _) x r) =
  (\l' -> blackDeleteLeftR l' x r) <$> extractMinR l

With all of this in place we then get the following function to delete an element from a RedBlackTree.

delete             :: Ord a => a -> RedBlackTree a -> RedBlackTree a
delete x (Tree bn) = case deleteB x bn of
                       BDeleted bn' -> Tree bn'
                       BShallow bn' -> Tree bn'

Note that we cannot move the Tree constructor, that occurs in both cases of the case distinction, before the case pattern, since the two cases produce values of a different type: the trees that they return have different black heights.

Concluding Remarks

We have seen how to enforce several properties of Red-Black trees in the type system. This gives us certain guarantees about the correctness of our implementation. However, you may have noticed that we still miss one property to provide us a proof that this implementation is correct. Namely, that the Red-Black tree is a binary search tree (i.e. for each node, the values in the left (right) subtree are smaller (larger) than the value stored in this node). So can we also enforce that in the type system? The answer is yes. To do this, we will need dependent types; types that depend on the values in our tree. This is currently possible, even in Haskell (using singletons), however at the moment that does not lead to very elegant code. Hopefully, this will improve in the future, so I can return to this at a later time.

Acknowledgments and Related Work

The implementation of the inserts is based on Okasaki’s famous work on purely functional Red-Black trees. I also looked at Stefan Kahrs and Matt Might’s implementations for inspirations on the delete operations. However, the setup with the types as I presented here requires fairly different code than that is used in their solutions.